本記事では、機械学習アルゴリズムの一種であるロジスティック回帰の振る舞いを解釈する方法について紹介します。
 桂川 大輝(カツラガワ ダイキ)
桂川 大輝(カツラガワ ダイキ)ロジスティック回帰
ロジスティック回帰とは、教師ありの機械学習アルゴリズムの一種で、分類や、その結果を予測する確率(予測確率)を算出します。例えば、顧客に対するアンケートから任意のセグメントを特定しているとき、そのデータに基づいてアンケートに回答していない人(顧客全体)の中からそのセグメントを予測するような場面での利用が考えられます。ロジスティック回帰は一般的に解釈性が高いとされています。常に当てはまるわけではありませんが、特徴量に対する回帰係数の大きさを特徴量の重要度として解釈できるためです。本記事では、具体的な例を用いてロジスティック回帰の振る舞いを解釈する方法を紹介します。
ロジスティック回帰による予測
まずは解釈する題材となる「ロジスティック回帰による予測」を実施します。以降、Pythonのスクリプトとサンプルデータによる例を提示しつつ説明します。実行環境はGoogle Colaboratoryで、Pythonのバージョンは3.8.10です(2023年03月01日現在)。
! python -version
Python 3.8.10
Google Colaboratoryですでにインストールされているライブラリに加えて、japanize_matplotlib、scikit-plotをインストールします。
!pip install japanize_matplotlib !pip install scikit-plot
以下のような簡単なサンプルデータを仮定します。
- サンプル
- 1,000件
- 目的変数(
label)- 「あるセグメント」か否かの2値(あるセグメント:1/あるセグメントではない:0)
- 「あるセグメント」の出現率(p)は10%
- 説明変数(
feature0、feature1、feature2、…feature9)- すべて数値
- 10件
- 欠損値、外れ値はない
サンプルデータを生成します。サンプルデータの生成はscikit-learnより、sklearn.datasets.make_classificationを利用します。
import random import pandas as pd from sklearn.datasets import make_classification RANDOM_STATE = 101 n_features = 10 feature_column_names = [f"feature{i}" for i in range(n_features)] label_column_name = "label" p = 0.1 n_samples = 1_000 random.seed(RANDOM_STATE) # 説明変数に対してランダムにスケールを調整する(0~10)の数値を掛ける random_numbers = random.sample(population=range(10), k=n_features) sample_classification = make_classification( n_samples=n_samples, n_features=n_features, n_classes=2, weights=[1 - p, p], random_state=RANDOM_STATE, scale=random_numbers, ) sample_df = pd.DataFrame(data=sample_classification[0], columns=feature_column_names) sample_df[label_column_name] = sample_classification[1]
以下のようなサンプルデータが生成されました。
sample_df.head()
| feature0 | feature1 | feature2 | feature3 | feature4 | feature5 | feature6 | feature7 | feature8 | feature9 | label | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0818149 | -7.93809 | 6.71572 | 0 | 16.5927 | 0.531373 | -5.37763 | -8.44793 | -6.25907 | -4.57904 | 0 |
| 1 | 2.88358 | 7.65834 | -0.240809 | -0 | -20.1159 | 2.6924 | -3.36721 | 10.0704 | 2.10784 | 1.70138 | 0 |
| 2 | -0.398732 | -0.134877 | 0.700138 | 0 | -6.00758 | -3.39811 | 0.901842 | 2.7964 | 17.4125 | -4.23657 | 0 |
| 3 | -0.331987 | -2.26738 | 3.94532 | 0 | -2.19203 | -0.59895 | -8.13409 | 0.827002 | 4.09391 | -5.89117 | 0 |
| 4 | 0.279755 | -5.12683 | 4.2682 | -0 | 9.94472 | 3.03352 | 10.9355 | -5.09538 | -3.47961 | -3.46767 | 0 |
サンプルデータの要約統計量は以下です。
sample_df.describe()
| feature0 | feature1 | feature2 | feature3 | feature4 | feature5 | feature6 | feature7 | feature8 | feature9 | label | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 |
| mean | 0.0530029 | -1.34656 | -0.0567591 | 0 | 0.262849 | 0.0284973 | 0.0404188 | -0.240234 | 0.561945 | -2.46408 | 0.104 |
| std | 0.999226 | 4.85797 | 4.09292 | 0 | 11.4055 | 2.07111 | 6.01835 | 5.73656 | 6.92895 | 3.24953 | 0.305413 |
| min | -3.46406 | -14.6063 | -12.8172 | 0 | -30.1574 | -6.80769 | -20.3308 | -15.3415 | -20.4585 | -12.1677 | 0 |
| 25% | -0.607474 | -4.89493 | -2.83305 | 0 | -8.77754 | -1.37508 | -4.16852 | -4.62929 | -3.98716 | -4.45224 | 0 |
| 50% | 0.0779487 | -1.80813 | -0.0951765 | -0 | 1.09257 | 0.112205 | -0.122587 | -0.617099 | 0.321718 | -2.77772 | 0 |
| 75% | 0.708417 | 2.02031 | 2.80951 | 0 | 9.05511 | 1.41489 | 4.02362 | 4.23623 | 5.35368 | -0.89181 | 0 |
| max | 3.35725 | 13.208 | 11.9476 | 0 | 30.0969 | 6.48637 | 18.4485 | 15.2479 | 21.3813 | 9.11678 | 1 |
サンプルデータをモデルに学習させます。モデルの評価のため学習データと検証データを分割し、学習データで学習させます。
from sklearn.model_selection import train_test_split X = sample_df.drop(columns="label") y = sample_df["label"] train_x, test_x, train_y, test_y = train_test_split( X, y, test_size=0.2, random_state=RANDOM_STATE, stratify=y )
それでは、ロジスティック回帰により学習をさせます。ロジスティック回帰はscikit-learnより、LogisticRegression(linear_model.LogisticRegression)を利用します。この時、「あるセグメント」か否かの割合(10%:90%)が不均衡であることを考慮しない場合、否という負例ばかり予測してしまうモデルになる恐れがあります。この時、class_weightというパラメータを"balanced"にすることで、クラスの出現率に反比例するように重みが自動的に調整されます。
from sklearn.linear_model import LogisticRegression model = LogisticRegression(class_weight="balanced", random_state=RANDOM_STATE) model.fit(train_x, train_y)
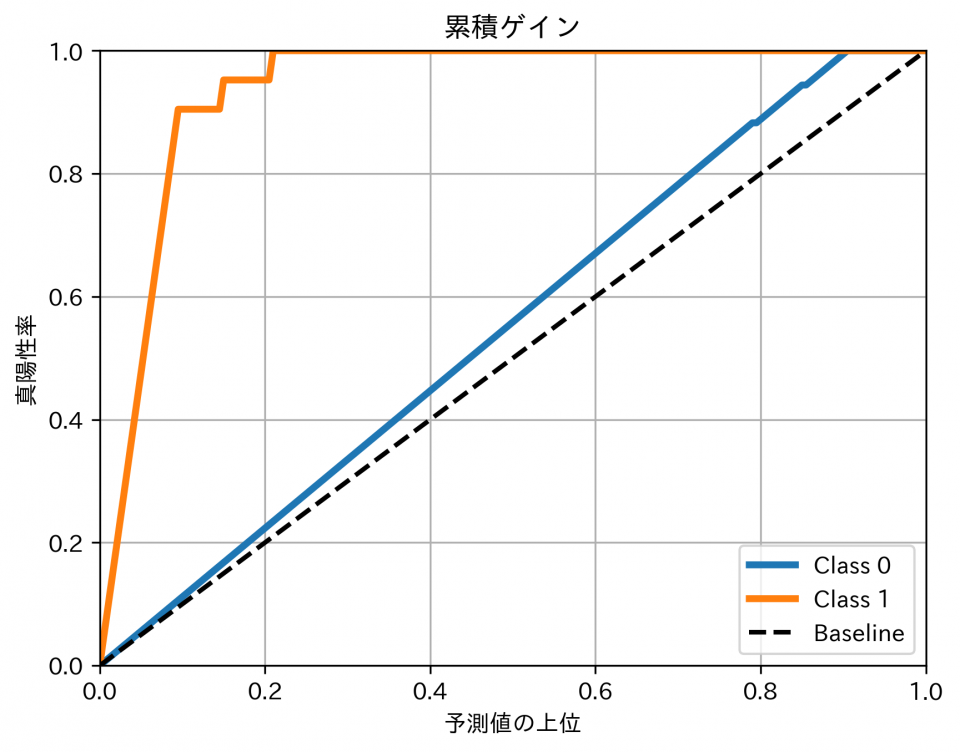
ここまでで、モデルの学習が完了しました。検証データを使って、予測性能を確認します。ここでは、累積ゲイン図による可視化により評価します。これにより「予測確率の上位何パーセントを抽出するとどれだけ予測の的中が見込めるか」ということを読み取りが可能です。累積ゲイン図はscikit-plot(scikitplot)により算出が可能です。
import japanize_matplotlib import matplotlib.pyplot as plt import scikitplot y_predict_proba = model.predict_proba(test_x) plt.rcParams["axes.axisbelow"] = True scikitplot.metrics.plot_cumulative_gain(test_y, y_predict_proba) plt.title("累積ゲイン") plt.xlabel("予測値の上位") plt.ylabel("真陽性率") plt.grid(visible=True) plt.rcParams["axes.axisbelow"] = False plt.show()
累積ゲイン図について、「あるセグメント(Class1)」の予測に対して、ランダムに予測した例(Baseline)と比べて上側にプロットされています。また、上位10%を選択した場合、真の「あるセグメント」が80%以上存在していること、上位20%を選択した場合に真の「あるセグメント」が80%以上存在していると読み取ることが可能です。このように、このモデルを使って、アノテーションをしていないデータに対しても、このような精度でラベルの分類および予測確率の算出が可能です。
ロジスティック回帰の解釈
ここまでで、ロジスティック回帰による分類を実施しましたが、この振る舞いを解釈する方法、活用する例を紹介します。
特徴量の重要度の算出(大局的な解釈)
ロジスティック回帰による分類を実現しましたが、その結果を活用する判断のために、モデルの振る舞いの「もっともらしさ」を知りたいという場面が考えられます。また、モデルの振る舞いから、分類において重要な特徴を特定し、施策の参考にしたいという場面が考えられます。そこで、ロジスティック回帰の回帰係数を確認することで解釈が可能です。回帰係数は特徴量と予測値の平均的な関係であり、「どの特徴量が強く影響するのか」、言い換えると特徴量の重要度の確認が可能です。
import matplotlib.pyplot as plt coefs = pd.DataFrame( data={"coef": model.coef_.squeeze().tolist()}, index=test_x.columns.tolist() ).sort_values("coef", ascending=True) plt.rcParams["axes.axisbelow"] = True plt.barh(coefs.index.to_list(), coefs["coef"].to_list(), align="center") plt.title("特徴量ごとの回帰係数") plt.xlabel("回帰係数") plt.ylabel("特徴量") plt.grid(visible=True) plt.show()
各特徴量のうち、feaure9の回帰係数が最も大きいことがわかります。したがって、「feaure9は予測の結果に対して重要な特徴量なのではないか?」ということが考えられます。しかし、変数間で比較した場合に、出力されている順で相関が高い変数なのかというと、そうとは限りません。各特徴量が取り得る値の範囲が異なるため、特徴量間で1単位増加したときの意味合いが異なるためです。
回帰係数を横並びで比較し、相関が高い順を確認するためには、学習データ、検証データの特徴量を標準化する必要があります。標準化はscikit-learnよりStandardScaler(preprocessing.StandardScaler)を利用します。標準化された特徴量から算出した回帰係数は標準偏回帰係数と呼ばれます。
学習データ、検証データを標準化します。
from sklearn.preprocessing import StandardScaler standard_scaler = StandardScaler() standard_scaler.fit(train_x) standard_train_x = pd.DataFrame( standard_scaler.transform(train_x), columns=train_x.columns ) standard_test_x = pd.DataFrame( standard_scaler.transform(test_x), columns=test_x.columns )
標準化した学習データをモデルに学習させます。
model = LogisticRegression(class_weight="balanced", random_state=RANDOM_STATE)
model.fit(standard_train_x, train_y)
検証データで予測性能を評価します。
import matplotlib.pyplot as plt y_predict_proba = model.predict_proba(standard_test_x) plt.rcParams["axes.axisbelow"] = True scikitplot.metrics.plot_cumulative_gain(test_y, y_predict_proba) plt.title("累積ゲイン(特徴量を標準化)") plt.xlabel("予測値の上位") plt.ylabel("真陽性率") plt.grid(visible=True) plt.show()
標準化は特徴量のスケールを変換するだけなので、予測精度への大きな影響はありません。
続いて、標準化したデータを学習したモデルの回帰係数を確認します。
import matplotlib.pyplot as plt coefs = pd.DataFrame( data={"coef": model.coef_.squeeze().tolist()}, index=test_x.columns.tolist() ).sort_values("coef", ascending=True) plt.rcParams["axes.axisbelow"] = True plt.barh(coefs.index.to_list(), coefs["coef"].to_list(), align="center") plt.title("特徴量ごとの標準偏回帰係数") plt.xlabel("標準偏回帰係数") plt.ylabel("特徴量") plt.grid(visible=True) plt.show()
標準化されたデータを学習したモデルの回帰係数ということもあり、それぞれは標準偏差分の値の変動がもたらす予測値への影響を意味します。つまり特徴量間での回帰係数の比較が可能になります。そして、標準化する前の結果と比較して、回帰係数の値や大小関係に変化があります。特に、回帰係数の内、feaure9が最も大きいということは変わりませんでしたが、feaure1とfeaure4の順序が変化しています。これにより、各特徴量の特性(スケールなど)の影響が考慮された比較における特徴量の重要度を示すことになっています。
個々の予測の根拠の算出(局所的な解釈)
ここまでで、特徴量の重要度を算出することで、ロジスティック回帰の振る舞いを解釈する方法を紹介しました。ただし、各顧客(個々のインスタンス)はそれぞれが異なる特徴を持ち、同じ予測結果になったとしてもさまざまな要因があったかと思われます。そこで、特定の顧客に対して、予測の根拠を特定したいという場面が考えられます。この要望に対してもロジスティック回帰の振る舞いの解釈の活用が可能です。ロジスティック回帰は回帰係数および切片を算出し、予測値を算出する回帰式の導出が可能です。そのため、観測値と回帰式を組み合わせることで予測結果の確認が可能です。
まずは、ロジスティック回帰モデルにおける回帰係数および切片を導出します(小数点第3位を四捨五入しています)。
# 回帰係数 [round(coef, ndigits=2) for coef in model.coef_.squeeze().tolist()]
[0.0, 0.39, -0.05, 0.0, 0.91, 0.03, -0.27, -0.82, -0.04, 3.28]
# 切片 round(model.intercept_.squeeze().tolist(), ndigits=2)
-2.21
これらから、今回のモデルは以下の回帰式での表現が可能です。
そして、適当なインスタンスを選択します。このインスタンスの予測の根拠を調べます。まずは、インスタンスの特徴量を取得します。
one_sample= standard_test_x.sample(n=1, random_state=101) one_sample.round(2)
| feature0 | feature1 | feature2 | feature3 | feature4 | feature5 | feature6 | feature7 | feature8 | feature9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 37 | 1.77 | 2.42 | -0.38 | 0.0 | -2.22 | 0.04 | -0.6 | 2.25 | 0.97 | 1.94 |
このインスタンスに対して予測確率を算出します。
y_predict_proba = model.predict_proba(one_sample) y_predict_proba_positive = y_predict_proba[0][1] round(y_predict_proba_positive, ndigits=2)
0.8
この約0.80という予測結果の根拠を調べます。ここまでで算出した、回帰係数とインスタンスの特徴量を掛け合わせて、予測値への影響がある項を確認します。
これらより、どの特徴量がどのように作用してこの結果となったかを読み取りが可能です。例えば、0.80という結果に対して、回帰係数が最も大きかったfeature9の項の正の影響が大きいということが読み取れます。このように、各インスタンスの予測の根拠の確認も可能です。また、「もし特徴量の値がこれだけ変わったら値はどのように変わるのか」といった問いの確認が可能です。
補足
ここまでで、ロジスティック回帰の振る舞いを解釈する方法を紹介しました。補足として、ここまでで注意することが望ましい点を紹介します。
回帰係数は予測値と特徴量の相関(因果を意味するとは限らない)
ロジスティック回帰の振る舞い、例えば回帰係数に基づいて「『あるセグメント』はこんな特徴がある」という仮説を立てることもあるかと思います。ここで注意が必要な点として、「『あるセグメント』の予測にある特徴量に比較的高い回帰係数が掛けられている」という事実に対して、『あるセグメント』とその特徴量間の関係は因果関係とは限らないという可能性があります。そのため、あくまで事実、およびこれから検証しようとする仮説までに留めておくことが望ましいです。
多重共線性の可能性
ロジスティック回帰のような複数の特徴量から目的変数を予測する回帰モデルにおいて、多重共線性(マルチコリニアリティ)という事象が生じることがあります。多重共線性とは特徴量間に強い相関がある事象です。特徴量間で相関が高い組み合わせが存在していたとします。そのとき、単体では目的変数の予測において重要な特徴量の回帰係数の一方が過大になり、他方が過小になってしまうという事象が発生することがあります。場合によっては本来は正の値となる回帰係数が負の値になることもあります。これにより、これら、回帰係数から特徴量と目的変数の関係を正しく解釈できなくなります。多重共線性を抑えるために、回帰係数の重みを制限する、特徴量を減らすなどという方法があり、これらを活用することで改善を試みることが可能です。
羅生門効果の可能性
同じデータセットに対して似たような性能を示す複数の回帰モデルが存在する場合、得られる示唆が異なるという場面があります。具体的には、ある設定や手法で「Aという特徴量が重要かもしれない」という示唆が得られたとして、他の設定や手法では「Bという特徴量が重要かもしれない」という異なる示唆が得られることがあります。これは羅生門効果と言われます。この時、受け取り手ごとに「納得できる」もしくは「都合の良い」解釈が異なるという場面が生じます。そのため、このような現象があることは理解した上での取り扱いへの注意が必要です。
おわりに
本記事では、ロジスティック回帰の振る舞いを解釈する方法を紹介しました。結果に納得し、意思決定を促すことを目標とするようなタスクでは、予測性能と解釈性のトレードオフを考える必要が生じます。このとき、予測性能が高い手法よりも解釈性が高い手法が有用な場面があり、機械学習アルゴリズムとその選定は興味深いですね。